Le protocole E91 implique deux acteurs principaux : Alice et Bob, qui jouent des rôles différents. Vous pouvez ici explorer l'ensemble des étapes que chacun d'eux doit suivre pour mener à bien le protocole.
Choisissez de façon aléatoire une base de mesure pour les photons incidents, les résultats de mesure seront utilisés pour établir votre clé de chiffrement et détecter la présence d'Ève.
Partagez vos bases de mesure avec Bob.
Extrayez votre clé de chiffrement à partir des résultats de mesure obtenus pour des paires de bases identiques.
Validez votre clé en testant l'inégalité de CHSH avec les mesures effectuées avec les autres combinaisons de bases.
Chiffrez et envoyez votre message à Bob.
Le protocole a été proposé en 1991 par Artur Ekert. Il implique deux parties distinctes, Alice et Bob, qui souhaitent établir une clé de chiffrement afin de communiquer de manière sécurisée via un canal public. Dans ce protocole, Alice et Bob reçoivent tous les deux un photon provenant d’une source qui émet des paires de photons dont les polarisations sont maximalement intriquées : les photons forment ce qu’on appelle des paires de Bell. Pour chaque paire, la polarisation d’un photon sera mesurée par Alice et l’autre par Bob. Alice effectue chaque mesure en choisissant de façon aléatoire une base parmi l’ensemble de trois bases {a, b, a'}. Bob fait de même en choisissant parmi les bases {b, a', b'}. Parmi les bases de mesure à leur disposition, Alice et Bob en ont donc 2 qu’ils partagent, b and a'.
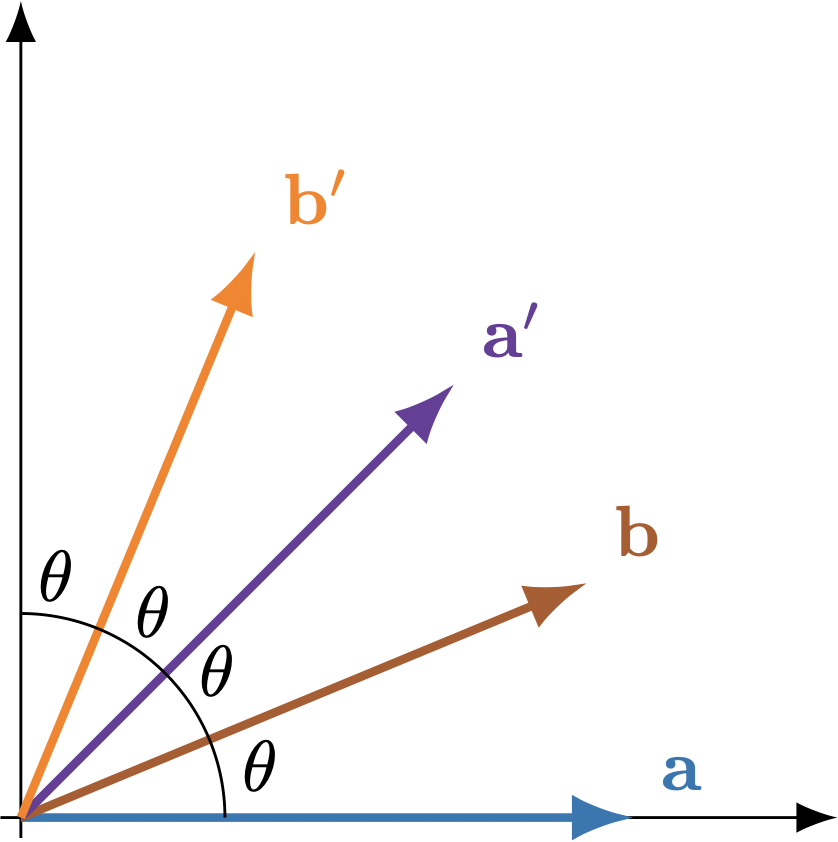
Pour chaque mesure, Alice et Bob enregistrent le résultat : +1 ou -1. Une fois la transmission des paires de photons terminée et les mesures effectuées, Alice et Bob divulguent les bases de mesure qu’ils ont utilisées pour chaque photon. Les résultats des mesures effectuées dans la même base sont conservés pour former la clé de chiffrement. Cette situation survient en moyenne 2 fois sur 9 : lorsqu’Alice et Bob mesurent tous les deux dans la base b ou encore dans la base a’. Les résultats des mesures effectuées dans des bases différentes sont révélés et utilisés pour valider la sécurité de la source et du canal quantique qui ont été utilisés. Pour ce faire, le protocole E91 s’appuie une des expériences les plus spectaculaires de la mécanique quantique : la vérification des inégalités de Bell. Il existe plusieurs formulations de ces inégalités et le protocole E91 s’appuie spécifiquement sur l’inégalité de CHSH. Alice et Bob travailleront seulement avec les résultats des mesures effectuées dans les bases suivantes
| Alice | Bob |
|---|---|
| a | b |
| a' | b |
| a | b' |
| a' | b' |
Ce sont donc, en moyenne, 4 paires de photons sur 9 qui sont utilisées pour vérifier l’inégalité de CHSH. Pour chaque paire de résultats issus des combinaisons de bases du tableau précédent, Alice et Bob calculent le produit mA × mB où mA et mB sont les résultats de la mesure effectuée par Alice et Bob respectivement. La moyenne des produits est ensuite calculée pour chacune des combinaisons de base.
En guise d’exemple, supposons qu’Alice et Bob ont effectué les mesures suivantes:
| Alice | Bob | \(m_{A} \times m_{B}\) | ||
|---|---|---|---|---|
| Base | mA | Base | mB | |
| a | +1 | b | +1 | +1 |
| a | +1 | b | -1 | -1 |
| a | -1 | b | -1 | +1 |
| a′ | +1 | b | +1 | +1 |
| a′ | -1 | b | +1 | -1 |
| a′ | +1 | b′ | +1 | +1 |
Le calcul des moyennes donne:
\[ E_{a,b} = \frac{1 - 1 + 1}{3} = 0.33 \] \[ E_{a',b} = \frac{1 - 1}{2} = 0 \] \[ E_{a',b'} = \frac{1}{1} = 1 \] \[ E_{a,b'} = 0 \]L’inégalité de CHSH consiste à vérifier que
\[ S = \lvert E_{a,b} + E_{a',b} + E_{a',b'} - E_{a,b'} \rvert \leq 2 \]Il s’avère que lorsque S est calculé à partir de photons intriqués, cette inégalité n’est pas vérifiée. En fait, on peut montrer que 𝑆 = 2√2 ≈ 2.83 pour des photons maximalement intriqués. Ainsi, si l’émetteur de paires de photons est fiable et que le canal de communication n’est pas bruité – ou pire espionné ! – Alice et Bob devraient observer que la valeur de S tend vers 2√2 au fur et à mesure qu’ils augmentent le nombre de paires de photons considérées dans leur calcul. Ils pourront alors utiliser la clé qu’ils ont obtenue pour chiffrer leur message. À l’inverse, si cette valeur demeure sous 2 ils ne peuvent avoir confiance en la clé obtenue et devraient s’abstenir de l’utiliser. Attention, les valeurs moyennes sont des quantités statistiques qui nécessitent un grand échantillon pour être significatives. Pour un nombre limité d’échantillons des anomalies statistiques peuvent survenir et il peut être difficile de tirer des conclusions.
Notez qu’il reste 3 combinaisons de bases de mesure qui ne sont pas utilisées dans le protocole E91 : (a, a'), (b, b'), and (b, a'). Les mesures effectuées avec ces paires de bases sont simplement jetées.